研究方向一：符号数值混合计算（Symbolic-numeric Hybrid Computing） 

• 　　研究内容 

　　数值计算采用有限精度浮点数近似计算，在工业和工程中广泛使用，效率高但误差累积造成精度有时过低，通常只能得到局部解。符号计算可以对带符号的数学表达式精确操作，能准确得到问题的全部解但受制于中间过程膨胀效率相对较低。如何结合高效但有误差的数值计算与精确但低效的符号计算获得满足目标精度的结果是符号数值混合计算的主要研究内容。 

• 　　创新成果 

• 　　基于同伦算法和临界点技术的的实代数簇连通分支样本点计算（图1） 

• 　　高维空间的稳定曲线追踪算法（图1） 

• 　　双参数多项式系统的边界曲线算法（图2） 

• 　　基于参数多项式系统求解的实同伦算法（图2） 

• 　　双参数多项式动力系统的Fold-Hopf分叉边界计算及在生物系统稳定性分析中的应用（图2） 

• 　　基于三角分解的实闭域一阶理论的量词消去算法（图3） 

• 　　含参程序的自动并行化（图4） 

图1 实连通分支样本点计算及曲线追踪 

图2 含参多项式系统求解及应用 

　　图3 实量词消去算法 

 图4含参程序的自动并行化 

• 　　发表文章 

　　研究方向二：零误差计算（ERROR-FREE NUMERICal COMPUTATION） 

• 　　研究内容 

　　数值计算方法不可避免地给计算结果带来多种误差，在航天航空、生物医疗等领域，计算误差可能会带来严重后果。符号计算可以得到问题精确地完备解，但是计算量大且表达式庞大，导致计算效率较低，或者受到计算机内存大小的限制而无法得到结果，往往不能满足实际问题求解的需要。据此，我们提出“零误差计算“的构想，即采用近似计算获得准确结果，研究结合兼具数值计算高效性和符号计算准确性的零误差数值计算高效算法. 特别地，对代数数的计算问题，我们提出了可充分保证计算结果无误差的浮点计算方法，在目前掌握的文献中，该方法计算量最小。相关成果在 ACM Communications in Computer Algebra、The 2014 International Workshop on Symbolic-Numeric Computation (2014年国际数学家大会卫星会议)，第六届全国计算机数学学术会议等期刊和会议上公开发表或报告。 

• 特色创新 

　　不同于美国纽约大学学者倡导的无限精度EGC模型，我们提出了“零误差计算”的概念。前期，已将有理数域上的零误差计算理论推广到了代数数域（一大类无理数），并从理论上保证中间计算过程采用有误差的数值计算，最终可得到无误差的结果（代数数GAP定理）。近期，在代数数恢复的误差控制方面取得新突破。主要是在符号计算国际顶级会议ISSAC 2014关于广义LLL格约化基最新结果的基础上，结合代数数GAP定理和矩阵计算中QR分解的误差估计方法，探明了计算过程中浮点位数的取值方法，可以充分保证计算结果的无误差。截至目前，已完成零误差计算关键算法 PSLQ 的数值稳定性分析（该算法曾被评为二十世纪十大算法之一）。据此，有望设计首个数值的PSLQ算法。 

• 　　项目支持 

• 　　采用数值计算求解一类半代数系统全部整数解，国家自然科学基金，2017年1月——2020年12月 

• 　　整数关系探测的误差可控算法与应用，国家自然科学基金，2016年1月——2018年12月 

• 　　零误差计算理论与应用，中科院“一三五”专项，2014年6月——2016年12月 

• 　　零误差计算在欧几里得格和密码学中的应用，重庆市基础与前沿研究计划，2013年12月——2017年12月 

　　研究方向三：因式分解（Factorization） 

• 研究背景 

　　随着信息技术的飞速发展，许多基于因式分解技术的密码方法应运而生。多项式分解问题作为代数运算理论和应用中的基本问题，同时它是一个符号计算在计算机代数领域成功应用的典范。在Maple以及Mathematica等相关数学软件中，因式分解已经作为一个标准功能被应用，但随着研究的深入，我们发现针对很多复杂案例的因式分解在理论以及算法的研究尚处于不完善阶段。 

•  多元数值因式分解理论研究   

• 与美国 Northeastern Illinois University 学者 Zhonggang Zeng 教授合作完成的数值多变元因式分解几何含意和几何结构分析，研究对该问题的几何背景做了深入分析，巧妙地将病态问题转化成了well-posed问题，同时给出了所有factorization manifolds的stratification结构以及数值因式分解的后向误差和条件数定理。 

• 在可充分保证计算结果无误差的浮点计算方法，并成功将其应用于多变元因式分解理论和算法分析，最新成果“The Numerical Factorization of Polynomials”发表在SCI一区刊物Foundations of Computational Mathematics。

•   

 二元因式分解数值求解问题 

• 利用稀疏性质，优化二元多项式因式分解算法 

• 算法效率上千倍高于计算机代数系统Maple中自带的因式分解命令 

　成果发表在 SCI 期刊 Science China Mathematics 和 J. System Scienc & Compleixty 上。

　研究方向四：同态加密及其应用（Homomorphic Encryption and Its Applications） 

• 研究背景 

　　同态加密是一种新型加密方案, 它可保证对密文进行直接运算解密的结果与对明文进行等价运算所得到的结果相同。所以它可以从根本上解决将计算委托给第三方时的保密问题，可满足传统加密方案所保障的通信安全和存储安全外的云端的运算安全。此外,它有望抵御量子攻击，是目前信息安全的前沿领域。 

• 　　研究进展 

　　中心从2013年开始对同态加密的研究工作，开发有若干基于同态加密的软件应用。HEBinCalc是我们基于IBM的HElib开发的同态整数运算库，该函数库利用HElib提供的二进制与运算(AND)和异或运算(XOR)，实现了在计算机上使用密文来进行不同进制下的加减乘除等算术运算的功能，可以灵活地选取数据位数，对大整数进行操作，加密数据可以进行存储或网络传输。运行库可以移植到各种服务器、PC以及嵌入式平台之上。目前该库在core i7 CPU的PC机上，可以在2.1s内完成16位的整数加减法。在此基础之上可以开发保密的数据通信及数据计算系统。

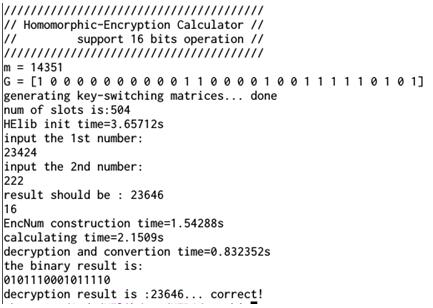
 同态整数运算库性能 

Arithmetic	Circuit	#bits	m	#slots	Lc	time(s)
Addition	RCA	16	14351	504	17	2.16
	CLA	16	7781	150	7	2.53
	CLA	64	13981	600	13	37.69
Subtraction	RCS	16	14351	504	17	2.17
	CLA	16	7781	150	7	2.52
	CLA	64	13981	600	13	37.16
Multiplication	RCA	8	8191	630	9	4.62
	RCA	16	14351	504	17	46.32
Division	RCA	4	18631	720	21	14.63

　　另外，我们基于该整数运算库，进一步开发了基于同态加密的电子投票系统演示平台，该平台利用同态加密技术进行选票的加密和计票过程，保证了投票过程的保密性，并利用时间戳和数字签名技术保证选票的安全性。 

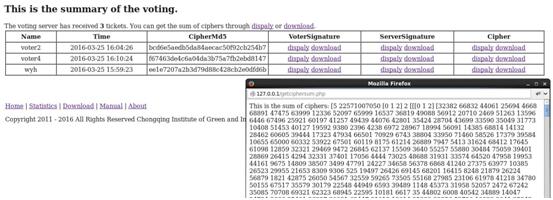
　　研究方向五：程序正确性验证（Verification of Program Correctness） 

• 　　研究背景 

　　随着计算机和互联网的迅猛发展，以通信、存储和计算为核心的信息基础设施已经渗透到政治、经济、军事、文化以及社会的各个层面。软件是信息基础设施的灵魂，但它并不总是让人信任，从而产生“软件可信性”问题。面向应用的程序正确性验证是可信软件基础研究的重要课题之一。其主要研究如何使用数学方法去证明给定程序是否符合预先设定的目标。研究内容包括：程序停机问题证明与不变式构造。 

• 　　创新成果 

• 　　将Tiwari提出的线性循环程序的终止性问题等价归约为两类特殊程序的终止性问题，并建立了终止性判定的递归算法。 

• 　　构造了线性程序不可终止点集合的实多面体吸引集。 

• 　　建立了基于不动点理论的多项式循环程序终止性判定理论。 

• 　　提出了L-depth Eventual 线性秩函数概念，证明了该函数与程序可终止性的内在关联。 

• 　　提出了微分不变式的新定义，丰富了不变式的表现形式。 

　　图1 线性程序多面体吸引集的半代数刻画 

　　图2 L-depth Eventual 线性秩函数 

• 　　发表文章 

联系人：吴文渊 邮箱：zidongtuili@cigit.ac.cn 网址：http://www.arcnl.org/