近日，重庆研究院自动推理与认知研究中心吴文渊团队在零误差计算的理论与应用方面取得突破，提出了可充分保证计算结果无误差的浮点计算方法，并成功将其应用于多变元因式分解理论和算法分析，系列成果发表在J. of Systems Science and Complexity和Science China Mathematics等刊物。最新成果“The Numerical Factorization of Polynomials”发表在SCI一区刊物Foundations of Computational Mathematics（DOI: 10.1007/s10208-015-9289-1）。 

　　目前计算机广泛采用的数值计算方法不可避免地给计算结果带来多种误差，这些误差可能会给航天航空、生物医疗等安全攸关领域，带来严重后果。因此，追求高精度、高效率的计算方法是科学计算的重要研究方向之一。不同于国外学者倡导的无限精度EGC模型，研究团队提出了“零误差计算”的概念，并已将有理数域上的零误差计算理论推广到了代数数域，从理论上保证中间计算过程采用有误差的数值计算，最终可得到无误差的结果。 

　　该最新成果是与美国 Northeastern Illinois University 学者 Zhonggang Zeng 教授合作完成的数值多变元因式分解几何含意和几何结构分析，研究对该问题的几何背景做了深入分析，巧妙地将病态问题转化成了well-posed问题，同时给出了所有factorization manifolds的stratification结构以及数值因式分解的后向误差和条件数定理 。 

　　SCI一区刊物Foundations of Computational Mathematics从2001年创刊至今共发表论文334篇, 此前以中国大陆学者为第一作者的论文仅有3篇（统计源于：　　http://link.springer.com/journal/volumesAndIssues/10208）。 

　　论文链接：http://link.springer.com/article/10.1007/s10208-015-9289-1 

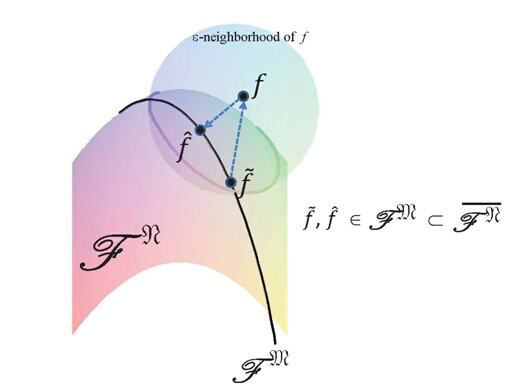
数值因式分解的几何基础：流形分层结构和病态问题的正则化方法